10進法 2進法 8進法 16進法 N進法

ここでは様々な基数の位取り法について、基礎的なことを説明します。 10進数と2進数の変換等、各基数の変換については（こちら）のリンク先を見てください。

目次

• 位取り記数法
• コンピュータや情報関係で使われる位取り記数法
• 10進法の数値と36進法の文字の対応表
• N進法の桁上がりアニメーション
• 数値の読み方について
• N進法のアバカス（算盤、そろばん） 4桁
• N進法の時計 4桁
• 10進数 2進数 8進数 16進数 N進数 比較カウンタ
• 10進数 2進数 8進数 16進数 N進数 対応表
• 基数変換
• 十進法 千進法 万進法 と 2進法 8進法 16進法
• ビットとバイト
• 接頭辞

位取り記数法

目次へ↑

私たちは普段、数を表記するのに「10進位取り記数法」略して「10進法」という位取り（くらいどり）記数法を使っています。 位取り（positional notation）というのは、数字の位置によって「1の位の桁」「10の位の桁」「100の位の桁」等の桁を扱うシステムのことです。 10進法では { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } の10文字をどの桁の位置に配置するかによって、大きな数や小さな数を簡単に扱うことができます。

10進法を使わなくてもちゃんと数を表すことができれば何を使っても問題ありません。 12進法や20進法が使われてる文化もあります。 現代でも時間や角度の「分」や「秒」には60進法が使われています。 12や60には約数が多いので、分割する際に便利に使われてきました。

私たちは子どもの頃からの教育で10進法を叩き込まれているため、他の位取り法を扱うときに戸惑ってしまいます。 手を動かしながらじっくり取り組み、しっかり理解していけば他の位取り法も必ず習得できます。 とりあえずは、「これまでの固定観念を取り除く頭の体操」のような感覚で取り組んでみてください。

コンピュータや情報関係で使われる位取り記数法

目次へ↑

位取り記数法の文字数に対応している数、つまり、桁の基準になる数のことを基数（radix 又は base）といいます。 基数が自然数Nである位取り記数法を「N進法」といいます。 コンピュータ関係では「2進法」「8進法」「16進法」がよく使われます。

2進法（Binary Numeral System）

基数2の位取り記数法

{ 0, 1 } の2文字を使う

「1」の次に桁が上がって「10」になる

2進法で表現された数値が2進数（Binary Number）

8進法（Octal Numeral System）

基数8の位取り記数法

{ 0, 1, 2, 3, 4, 5, 6, 7 } の8文字を使う

「7」の次に桁が上がって「10」になる

8進法で表現された数値が8進数（Octal Number）

10進法（Decimal Numeral System）

基数10の位取り記数法

{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } の10文字を使う

「9」の次に桁が上がって「10」になる

10進法で表現された数値が10進数（Decimal Number）

16進法（Hexadecimal Numeral System）

基数16の位取り記数法

{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f } の16文字を使う

「f」の次に桁が上がって「10」になる

16進法で表現された数値が16進数（Hexadecimal Number）

10進法は10が基数で「束（たば）にしてまとめない1の桁」「10個を一束にまとめた、10の桁」「10の桁10個を一束にまとめた、100の桁」「100の桁10個を一束にまとめた、1000の桁」「…」を並べて数を表現します。 2進法は2が基数で「束にしてまとめない1の桁」「2個を一束にまとめた、2の桁」「2の桁2個を一束にまとめた、4の桁」「4の桁2個を一束にまとめた、8の桁」「…」を並べて数を表現します。 このような束の階段は累乗指数を使うと綺麗に表現できます。

2進法を使うのは ｛電圧の高い，低い｝や ｛磁石の上向き，下向き｝や ｛光が反射する，反射しない｝ 等の現象を使って情報の違いを明確に表すのに便利だからです。 8進法と16進法に関しては2進法と相性が良いという理由でよく使われます。 2進法は使う文字が少ないため、10進法の九九に対応するものが 1× 1=1 しかありません。 少ない計算ルールを実現する単純な電気回路の組み合わせで、複雑な計算が可能になります。 単純な機械が処理するのに丁度良い位取り法というわけです。 しかし大きな数を扱うとなると、桁数がとても多くなり、人間が扱うには不向きです。 そこで、10進法に基数が近く、しかも2進法とも相性が良い8進法や16進法が便利になってくるわけです。

10進法の数値と36進法の文字の対応表

目次へ↑

私たちが普段使っている数字は「アラビア数字」別名「算用数字」「インド数字」と呼ばれているもので、{ 0, 1, …, 9 } の10文字だけを使って数を表現します。

歴史的には6世紀ごろのインドで、空位を表す「0」の発見があり、「0」を含めた数の足し算や掛け算等の計算規則が確立したことによって、現在用いているような位取り記数法が成立するようになりました。 インドで確立した数字と位取り記数法は、8世紀ごろにはアラビア半島に、11世紀ごろにはヨーロッパに伝わったと言われています（参考）。 その間に数字の形の変遷がありましが、16世紀ごろのヨーロッパにおける印刷技術や活字の発達によって、現在の数字の形に固定されたと考えられます。

実は紀元前20世紀ごろ、古代バビロニアでは楔形文字で表された60進法による位取り記数法が使われていました（参考）。 60には約数が多いので分割を扱うのに便利で、その後も60進法で表された小数が古代ギリシャの数学や天文学に引き継がれます。 60進法の小数は中世のアラビアやヨーロッパの天文学にまで引き継がれましたが、60進法は九九の扱いが難し過ぎて一部の専門家しか扱えない代物でした。 また、16世紀に10進法の小数がヨーロッパのステヴィン等によって発明されたことによって60進法は使われなくなっていきます。 今でも時間や角度の扱いに60進法の名残がありますが、それ以外に60進法を使うことは滅多にありません。

アラビア数字しか使えない場合、基数が10以上になると数字の位置だけで桁を表すことができなくなり、どうしても補助的な単位や記号が必要になってしまいます。 例えば、60進法では、「分」や「秒」といった単位を補って「36分45秒」と表記したり、記号を補って「36'45''」や「36:45」などと表記したりする必要があります。

使用する文字数を増やして、1文字で表せる数を大きくすれば良いと良いと思われるかも知れませんが、やりすぎると位取り記数法のメリットがなくなってしまいます。 あまりにも1桁の数が大きくなりすぎると、数値の大きさの順番を暗記するだけでも大変です。 1文字で表せる数を大きくするにしても、誰でも順番を知っている文字を使う必要があります。

よく使われるのは、英語のアルファベット { a, b, …, z } の26文字です。 これなら世界中の殆どの人が順番を知っているので、アラビア数字10文字と組み合わせて計36文字まで使うことができます。 以下は10進法の数値と36進法の文字の対応表になりますが、わざわざ表にしなくても何となく順番が分かるのではないでしょうか？

2進法～36進法を用いて、どのように数を表したり数えたりすることができるのか？ この後のプログラムを動かしてみて実感してみましょう。

N進法の桁上がりアニメーション

目次へ↑

まずは、桁上がり（繰り上がり）の感覚を掴んでおくと良いでしょう。 ここの装置を利用して、1つずつ数を[ + ]しながら、桁上がりの様子をじっくり観察してみてください。 [2]進法になっている基数の部分を、様々に変えてやってみましょう。 「それぞれの桁に基数N個の玉が溜まっていたら、一塊の束にして次の桁の一個の玉に置き換える」という桁上がりの作業をアニメーションで表示します。

上のプログラムは、様々な基数（2から36）の位取りを、桁（位）ごとに色が違う玉の数で表現するものです。 一個ずつ玉を積み上げて、桁上がりの作業をアニメーションで表示します。 操作法は以下の通りです。

• ボタン[ + ]で数値を1つ増やして玉を積み上げます。
• [2]進法の基数、[D3]色の玉の色、の部分には自分の好きな値を選択します。
• [set 0]ボタンで数値を0にします。
• [N]進法の右の数値には、10桁までの制限で自分の好きな値を入力できます。入力後に[set]ボタンを押してください。

[2]進法では「11...1」のような連続「1」を、[8]進法では「77...7」のような連続「7」を、[10]進法では「99...9」のような連続「9」を、[16]進法では「ff...f」のような連続「f」を、[N]進法では連続する「N-1」、を[set]して、[ + ]ボタンで数値を1つ増やしてみましょう。 連続桁上がりのアニメーションが観察できます。

[10]進法の例では、色違いの玉をそれぞれ「一円玉」「十円玉」「百円玉」「千円札」「一万円札」と考えてみてください。 普段何気なくやっている「一円玉10個で十円玉に置き換える」「十円玉10個で百円玉に置き換える」「百円玉10個で千円札に置き換える」「千円札10個で一万円札に置き換える」「…」という感覚で桁上がりを理解できます。

基数が変わっても同じように考えればよく「ある桁に基数個の玉が溜まっていたら、それを次の桁の玉に置き換える」という作業を行います。

[2]進法の例では、色違いの玉をそれぞれ「一円玉」「二円玉」「四円玉」「八円玉」「十六円玉」と考えてみてください。 「一円玉2個（2進表記10個）で二円玉に置き換える」「二円玉2個（2進表記10個）で四円玉に置き換える」「四円玉2個（2進表記10個）で八円玉に置き換える」「八円玉2個（2進表記10個）で十六円玉に置き換える」「…」という感覚で桁上がりを理解できます。

[8]進法の例では、色違いの玉をそれぞれ「一円玉」「八円玉」「六十四円玉」「五百十二円玉」「四千九十六円玉」と考えてみてください。 「一円玉8個（8進表記10個）で八円玉に置き換える」「八円玉8個（8進表記10個）で六十四円玉に置き換える」「六十四円玉8個（8進表記10個）で五百十二円玉に置き換える」「五百十二円玉8個（8進表記10個）で四千九十六円玉に置き換える」「…」という感覚で桁上がりを理解できます。

[16]進法の例では、色違いの玉をそれぞれ「一円玉」「十六円玉」「二百五十六円玉」「四千九十六円玉」「六万五千五百三十六円玉」と考えてみてください。 「一円玉16個（16進表記10個）で十六円玉に置き換える」「十六円玉16個（16進表記10個）で二百五十六円玉に置き換える」「二百五十六円玉16個（16進表記10個）で四千九十六円玉に置き換える」「四千九十六円玉16個（16進表記10個）で六万五千五百三十六円玉に置き換える」「…」という感覚で桁上がりを理解できます。

[N]進法の例では、色違いの玉をそれぞれ「一円玉」「N円玉」「N²円玉」「N³円玉」「N⁴円玉」と考えてみてください。 「一円玉N個（N進表記10個）でN円玉に置き換える」「N円玉N個（N進表記10個）でN²円玉に置き換える」「N²円玉N個（N進表記10個）でN³円玉に置き換える」「N³円玉N個（N進表記10個）でN⁴円玉に置き換える」「…」という感覚で桁上がりを理解できます。

様々な基数のN進法で、2つの数の足し算の実行を視覚化したアニメーションプログラムが（こちら）にあります。

数値の読み方について

目次へ↑

10進法では 「0（ゼロ）」 「1（イチ）」 「2（ニ）」 ・・・ 「9（キュー）」の次に桁上がりが起こって 「10（イチ・ゼロ_{、又は、ジュウ}）」になります。 普段使い慣れてるので問題ないと思います。 普段使っている数値の命名規則も10進法で最適化されています。 子供のころから頭に叩き込まれて使い慣れすぎているため、他の位取り法に移行するのが大変ですが要は慣れの問題です。

2進法では 「0（ゼロ）」 「1（イチ）」の次に桁上がりが起こって 「10（イチ・ゼロ_{、又は、ニ}）」になります。 次に 「11（イチ・イチ_{、又は、サン}）」ときて、その次の数は桁上がりが続けて起こって 「100（イチ・ゼロ・ゼロ_{、又は、ヨン}）」になります。 どんな風に桁上がりが起こるのかを意識しながら何度もトライしてみてください。 桁上がりの感覚がつかめてくると、ちょっとだけ楽しくなってきます。

8進法では 「0（ゼロ）」 「1（イチ）」 「2（ニ）」 ・・・ 「7（ナナ）」の次に桁上がりが起こって 「10（イチ・ゼロ_{、又は、ハチ}）」になります。 次に 「11（イチ・イチ_{、又は、キュー}）」 「12（イチ・ニ_{、又は、ジュウ}）」 ・・・ 「17（イチ・ナナ_{、又は、ジュウゴ}）」ときて、その次に桁上がりが起こって 「20（ニ・ゼロ_{、又は、ジュウロク}）」になります。

16進法では 「0（ゼロ）」 「1（イチ）」 「2（ニ）」 ・・・ 「9（キュー）」の次に桁上がりが起こらず 「a（エイ_{、又は、ジュウ}）」になります。 次に 「b（ビー_{、又は、ジュウイチ}）」 「c（スィー_{、又は、ジュウニ}）」 「d（ディー_{、又は、ジュウサン}）」 「e（イー_{、又は、ジュウヨン}）」 「f（エフ_{、又は、ジュウゴ}）」ときて、その次に 「10（イチ・ゼロ_{、又は、ジュウロク}）」に桁上がりします。 次に 「11（イチ・イチ_{、又は、ジュウナナ}）」 「12（イチ・ニ_{、又は、ジュウハチ}）」 ・・・ 「1e（イチ・イー_{、又は、サンジュウ}）」 「1f（イチ・エフ_{、又は、サンジュウイチ}）」ときて 「20（ニ・ゼロ_{、又は、サンジュウニ}）」に桁上がりします。

ここでは数の読み方をカタカナで（）内に書きました。 小さい字の「_又は」の右にはその数に対する日本語の固有名詞を書きました。 固有名詞とは対象のものに与えられた名前のことで、日本語の数の命名規則には10進法が使われています。 他の基数で表現されている数値に通常の固有名詞を用いると、ややこしくなってしまいます。 普段は 「20a5（ニ・ゼロ・エイ・ゴ）」のように桁ごとに一文字ずつ読むことにして「必要な時に対応する10進数に読み替える」という扱いをすると良いでしょう。

N進法のアバカス（算盤、そろばん） 4桁

目次へ↑

別の装置でも、桁上がりの感覚を掴むことができます。 ここの、そろばんのような装置、を利用して、1つずつ数を[ + ]しながら、数えてみてください。 [10]進法になっている基数の部分を、様々に変えてやってみましょう。

上のプログラムは、様々な基数（2から36）の4桁の数を、4色の珠で表現するものです。 操作法は以下の通りです。

• ボタン[ + ]で数値を1つ増やします（カウントアップ）
• ボタン[ - ]で数値を1つ減らします（カウントダウン）
• [10]進法の基数、[D3]色の針の色、の部分には自分の好きな値を選択したり入力します。
• [all 0]ボタンで4桁全ての値を0にし、[randam]ボタンで4桁全ての数値をランダムな値にします。
• 背景色が付いた4桁のディジタル表示の部分には、自分の好きな数値を入力できます。入力後に[set]ボタンを押してください。

アバカス（abacus）とは古くから使われていた計算器具で、その起源は紀元前2700年ごろのメソポタミア文明に遡ると言われています。 桁の概念を具現化しており、この道具が位取り記数法の起源になっているとも考えられます。 現在の算盤（そろばん）はアバカスを原型として、それが東洋に伝わる過程で様々な改良がおこなわれたものだと考えられます。 古代ローマ帝国ではアバカスに使われていた小石の珠を calculs と呼んでいて、これが英語の計算（calculation）の語源になっています。

10桁バージョンのN進アバカスが（こちら）にあります。

N進法の時計 4桁

目次へ↑

別の装置でも、桁上がりの感覚を掴むことができます。 ここの時計のような装置、を利用して1つずつ数を[ + ]しながら、数えてみてください。 [12]進法になっている基数の部分を、様々に変えてやってみましょう。

上のプログラムは、様々な基数（2から36）の4桁の数を4本の針で表現する時計のような装置です。 操作法は以下の通りです。

• ボタン[ + ]で数値を1つ増やします（カウントアップ）
• ボタン[ - ]で数値を1つ減らします（カウントダウン）
• ボタン[ ++ ]で数値を自動で1つずつ増やします
• ボタン[ -- ]で数値を自動で1つずつ減らします
• ボタン[stop]で自動更新を中断します
• [12]進法の基数、[D3]色の針の色、チックタック（tiktac）の更新時間、の部分には自分の好きな値を選択したり入力します。
• [all 0]ボタンで4桁全ての値を0にし、[randam]ボタンで4桁全ての数値をランダムな値にします。
• 背景色が付いた4桁のディジタル表示の部分には、自分の好きな数値を入力できます。入力後に[set]ボタンを押してください。

この時計では長さと色が違う4本の針で、N進法の4桁を表現します。 ある針の1周分の数をまとめて次の針に引き継ぐという操作が、数の束をまとめて新しい桁を作るという桁上がりの操作に対応します。

通常の時計では、秒針の60秒で1分の単位に、長針の60分で1時間の単位に、短針の12時間で半日の単位になります。 複雑な時間の単位の変遷に比べると、N進法の桁の扱いは単純な仕組みであることが分かります。

ちなみに（こちら）で負の整数についての補数による表現法をしっかり学んだ後で、[all 0]から[-]で逆回転させてみましょう。 4桁の補数表現の意味をより深く知ることができます。

10桁バージョンの10針のN進法時計が（こちら）にあります。

10進数 2進数 8進数 16進数 N進数 比較カウンタ

目次へ↑

次に基数が違う数表現の比較をします。 次のN進法比較カウンタを利用してください。 1つずつ数を増やしたり減らしたりしながら桁上がりの違いに注目して、何回も繰り返し数を数えてみましょう。

上のカウンタの操作法です。

• ボタン[ + ]で数値を1つ増やします（カウントアップ）
• ボタン[ - ]で数値を1つ減らします（カウントダウン）
• ボタン[ ++ ]で数値を自動で1つずつ増やします
• ボタン[ -- ]で数値を自動で1つずつ減らします
• ボタン[stop]で自動更新を中断します
• 10進数の初期値、[2,8,16]進数の基数、自動更新時間、の部分には自分の好きな値が入力可能で、入力後[set]ボタンで設定変更できます

10進数 2進数 8進数 16進数 N進数 対応表

目次へ↑

以下に10進数、2進数、8進数、16進数の対応表を示します。 桁上がりを意識して、数を数えながらスクロールバーを下して適当なところまで眺めてください。 表の横に並んでる数は見た目は違いますが同じ数を表しています。 例えば10進数の11と、2進数の1011と、8進数の13と、16進数のbは同じ数を表しています。

基数変換

目次へ↑

基数を変えるにはちょっとした変換計算を行います。 この変換計算のことを基数変換といいます。 情報系の資格を取る人はどんな値でも変換計算できるようにしておくことが重要です。 （基数変換）のリンク先で手計算でのやり方を説明します。 変換計算ができるようになると、コンピュータの気持ちが分かるようになります。

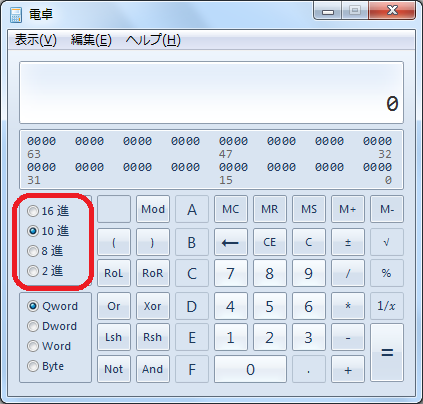
Windows アクセサリの「電卓」アプリには、[表示(V)]→[プログラマ(P)]とクリックすることでプログラマ電卓を利用できます。 [10進]状態で数値を打ち込んで[2進]のラジオボタンを押せば10進数を2進数に変換できます。 答え合わせに利用すると良いでしょう。

十進法 千進法 万進法 と 2進法 8進法 16進法

目次へ↑

桁数が大きな場合、いくつかの桁を塊にまとめるとすっきりします。 様々な文化による違いはありますが、大きな桁数の数を扱うときは、補助的な単位や区切り記号を使ってきました。

十進法を3桁ずつにまとめると千進法になりますが、こちらは英語を含むヨーロッパ系の言語での数の命数法によく使われています。 また、簿記や会計では3桁毎にカンマ記号で桁を区切って数値を表示することが多いです。

十進法を4桁ずつにまとめると万進法になりますが、こちらは日本語を含む漢字圏での数の命数法によく使われています。 また、現在あまり使われていませんが、4桁毎にカンマで桁を区切って数値を表示すると、日本人にとって分かりやすくなって、すぐに数値を読むことができます。

同じように2進法を3桁ずつにまとめたものが8進法で、4桁ずつにまとめたものが16進法に相当します。 2進法ではすぐに桁が大きくなってしまうので、8進法や16進法で表現した方が扱いやすいことが多いです。

以下のように空位に0を補った3桁での2進数と8進数の対応や、4桁での2進数と16進数の対応の表を作っておくと、互いの基数変換に便利です。

以下のような表を作ると、8進法と16進法の違いは、千進法と万進法の違いのようなものだと理解できます。

ビットとバイト

目次へ↑

2進数の1桁のことを1ビット（bit：binary digit の略）と呼びます。 2進数を数桁をまとめたものを1バイト（byte）と呼びます。 byte の元々の意味は「噛む、食いつく」です。 1バイトはコンピュータが一回で処理するデータ量を表す基本単位でした。 コンピュータの黎明期では1バイトが6ビットだったり7ビットだったりしていましたが、そのうち8ビットが主流になりました。 その後処理の基本単位が16ビットや32ビットに拡張されていきましたが、8ビットで1バイトというのが世界中に広まってしまったので、現在では8ビット1バイトになっています。 8ビットで1バイトが正式に決められたのは2008年になります。 正式に決められるまでに時間がかかったので、誤解を避けるために8ビットのことを1バイトという言い方を避けて、オクテット（octet）という言い方をすることがあります。

ビット(bit)の省略表記には「小文字の b」が使われます。 バイト(Byte)の省略表記には「大文字の B」が使われます。

10進法と2進法の基数変換にはちょっとした変換計算が必要です。 ところが、2進法、8進法、16進法の基数変換には変換計算が必要ありません。 対応表を見ると分かると思いますが、2進法を3桁の塊でみれば8進法、2進法を4桁の塊で見れば16進法になります。 （これは 2³ = 8、 2⁴ = 16 の関係があるからです。） 「2進法の3桁と8進法の1桁の対応表」、「2進法の4桁と16進法の1桁の対応表」があれば何桁の数でも計算せずに対応が分かるというわけです。 2進法では表示するのに桁数が沢山必要です。 人間が扱うには2進法よりも8進法や16進法の方が、数の大きさが10進法により近くて扱いやすいです。

16進法は2桁で丁度1バイト（8ビット）になるので16進法は2桁の塊で扱うことがよくあります。 文字コードやカラーコードやコンピュータの内部メモリの表現等に使われます。

接頭辞

目次へ↑

接頭辞 (prefix) とは、単語の頭にひっつけて、続く単語を修飾（説明したり、変化させたり、強調したり、限定したり）する言葉です。接頭語ともいいます。

数に関しても様々な接頭辞があります。

SI接頭辞

国際単位系（SI）では 長さの単位 m（メートル）の前に c（センチ）をつけて cm （センチメートル）とすることで、百分の一メートルを表すことになります。 メートルの単位に乗数 10^-2 を掛け算した単位、つまりメートルの百分の一の単位になるということです。 この接頭辞を使うことで、大きな単位や小さな単位をスッキリと表現することになります。 主なSI接頭辞を表にすると以下のようになります。

2進接頭辞

コンピュータ関係や情報系では2進法のための2進接頭辞というものが使われます。 接頭辞は 2¹⁰=1024 倍ごとに名称がつけられています。 これはSI接頭辞の1000倍に一番近い値を採用したからです。 1KB（一キロバイト）は 1024B（千二十四バイト）、1MB（一メガバイト）は 1024KB（千二十四キロバイト）、つまり 1024²B = 1048576B（百四万八千五百七十六バイト）になります。 主な2進接頭辞を表にすると以下のようになります。 名称はSIと同じ名称を使います。 記号のキロに関しては大文字を用います。 同じ名称ですが、大きな単位になっていくとSIとの乖離が大きくなります。 キロでは2.4%程度2進接頭辞の方が大きいだけなのですが、ヨタになると20.9%も2進接頭辞の方が大きくなります。