関数とは
中学校、高校の数学で関数(function)というものを習っていると思います。
関数は論理や数学や情報の基礎に関わる非常に重要な概念です。
関数は非常にシンプルな概念で、そのシンプルさ故に応用範囲がむちゃむちゃ広いです。
これまでなんとなく理解していた人も、ここで一度立ち止まってしっかり考えてみてください。
関数を理解していることで、その後の様々な学習の理解度がかなり変わってきます。
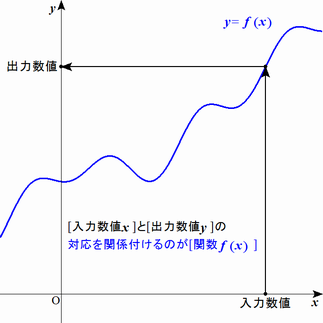
関数とは数値の間の対応関係です。
入力数値を $x$ で表します。
出力数値を $y$ で表します。
$x$ と $y$ がどのような関係になってるかというルールを $f$ で表します。
\begin{align*}
\mbox{入力数値}\quad x \quad\xrightarrow[\mbox{関係ルール}]{f}\quad y \quad\;\mbox{出力数値}
\end{align*}
ちなみに数学では $x$ を独立変数(independent value)、$y$ を従属変数(dependent value)といいます。
独立(independent)・従属(dependent)、よりも入力(input)・出力(output)の方がイメージしやすいです。
入力値・出力値は様々な値に変わるので変数というイメージは持っていてください。
ルールの $f$ の表現(記述)の仕方にはいろいろあります。
- 数式で表現
- 数表で表現
- グラフで表現
- プログラム言語で表現
- 言葉で表現
- 関数名で表現
どのような記述でも構いません。
(数学的に厳密な議論をするときは曖昧な表現は避けなければいけないけど。)
重要なことは $x$ の値を決めれば $y$ の値が1つに定まる ということです。
「$f$ というルールで $x$ と $y$ の関係がつきます」ということを数式で表現したものが以下の式になります。
\begin{align*}
y = f(x)
\end{align*}
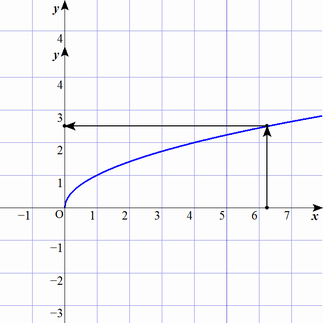
グラフで表現した一例が以下の図になります。
関数 $f$ の入出力のルールの記述には様々な表現が可能です。
以下の表現は全て同じ関数を表しています。
- 言葉で表現
$f$ は $x$ が $1$ 増えると $y$ は $2$ 増えて、$x$ が $0$ の時 $y$ は $3$ である関数
- 数式で表現
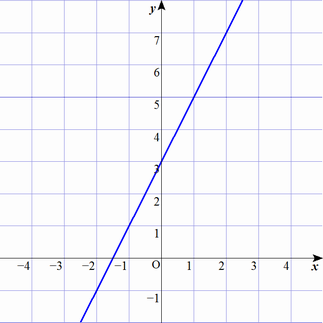
$f(x) = 2x+3$
- 数表で表現
$f$ は次の数表で表される関数(この表現には精度の問題がある)
| $x$ | $\cdots$ | $-2.0$ | $-1.5$ | $-1.0$ | $-0.5$ | $0.0$ | $0.5$ | $1.0$ | $1.5$ | $2.0$ | $\cdots$ |
| $y$ | $\cdots$ | $-1.0$ | $0.0$ | $1.0$ | $2.0$ | $3.0$ | $4.0$ | $5.0$ | $6.0$ | $7.0$ | $\cdots$ |
- 図で表現
$f$ は次のグラフで表される関数(この表現では、全領域を描ききれてない)
数式で関数を表現できれば綺麗で曖昧さも少なくて良いのですが、いつでも数式で書けるとは限りません。
同じ機能(同じ入出力関係)の関数でも表現方法は様々だと思っていてください。
中学高校で習う関数の例
無限の種類の関数があります。
わざわざ名前を付ける必要がないものは $f(x)$ とか $g(x)$ とか $h(x)$ とかで表現します。
一次関数($a, b$ を定数として、変数 $x$の一次式で表される)
\begin{align*}
f(x)=ax+b
\end{align*}
二次関数($a, b, c$ を定数として、変数 $x$の二次式で表される)
\begin{align*}
f(x)=ax^2+bx+c
\end{align*}
定数とは値が定まってる数(特定の数値)のことです。
変数とは値が定まっていない数のことで、$x$ に具体的な数を入力して初めて値が定まる数です。
有名な関数には名前がついています。
正弦(sine)関数
\begin{align*}
\sin (x) \: & = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!}x^{2n+1} \\
&= x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 - \frac{1}{7!}x^7 + \cdots
\end{align*}
余弦(cosine)関数
\begin{align*}
\cos (x) \: &= \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n)!}x^{2n} \\
&= 1 - \frac{1}{2!}x^2 + \frac{1}{4!}x^4 - \frac{1}{6!}x^6 + \cdots
\end{align*}
ここでは数式で表現しましたが、微分を習得しないと理解できません。
実用や応用には数表の表現で十分です。
昔の数学の教科書には必ず数表がついていました。
今は、関数電卓、パソコンやスマホのアプリ、を使うと良いです。
関数の特徴や性質
「関数の特徴や性質」が重要になることがあります。
その関数にどんな特徴があるのか知っておくと応用に便利です。
例えば、1次関数 $y=f(x)=ax+b$ には次のような性質があります。
- 定数 $a$ が正の値なら 「$x$ が増えれば $y$ も増える単調増加関数」
- 定数 $a$ が負の値なら 「$x$ が増えれば $y$ が減る単調減少関数」
2次関数 $y=f(x)=ax^2+bx+c$ には次のような性質があります。
- 定数 $a$ が正の値なら「頂点で下に凸(凹)になる関数」
- 定数 $a$ が正の値なら「頂点で上に凸(凸)になる関数」
正弦関数 $y=\sin(x)$ や余弦関数 $y=\cos(x)$ 等の三角関数には次のような性質があります。
- 入力 $x$ が $360^\circ$ 増えると 出力 $y$ の値や増減が同じになるという周期性を持つ関数
関数を組み込んだ数式
関数を組み込んだ数式を扱うこともあります。
「$f(x)+2g(x)$」や「$\sin(x)\cos(x)$」等です。
関数の位置には、その関数の出力数値を当てはめるということになります。
入力値 $x$ の値が具体的に確定していない時は「$x$ の値が確定した瞬間に、そこに当てはまる数値が確定する」という感じでいてください。
$f(x)=x+1,\;g(x)=x^2 + 3$ とする。
\begin{align*}
x = 1\, \mbox{の時}\; f(1) = 1 + 1 = 2,\; g(1) = 1^2 + 3 = 4
\end{align*}
\begin{align*}
f(1) + 2 g(1) = 2 + 2\cdot 4 = 10
\end{align*}
\begin{align*}
x = 30^\circ \mbox{の時、三角関数表より}\; \sin\left(30^\circ\right) = 0.500, \; \cos\left(30^\circ\right) = 0.8660
\end{align*}
\begin{align*}
\sin\left(30^\circ\right)\cos\left(30^\circ\right) = 0.5000\cdot 0.8660 = 0.7310
\end{align*}
関数と関数の関係
「関数と関数の関係」が重要になることがあります。
恐らく公式を覚えるのに一生懸命で、関数とはあまり意識せずに扱っていたと思います。
以下の例は「入力値 $x$ がどんな値でも同じ数値を入力したなら、$\sin(x)$ の出力の2乗と $\cos(x)$ の出力の2乗の和は必ず$1$である」
ということを表しています。
\begin{align*}
\left\{\sin(x)\right\}^2+\left\{\cos(x)\right\}^2 = 1
\end{align*}
以下の例は「$x$ を正弦関数に入力したときの出力と、$90^\circ - x$ を余弦関数に入力したときの出力は同じである」
ということを表しています。
\begin{align*}
\sin\left(x\right)=\cos\left(90^\circ - x\right)
\end{align*}
上の方にも書きましたが、関数の数の対応で1つだけ重要な注意があります。
「$x$ の値を決めれば $y$ の値が1つに定まる」ということです。
「$y$の値が2つとか3つになってどれを出力に定めたらよいのか決まらない」のはダメということです。
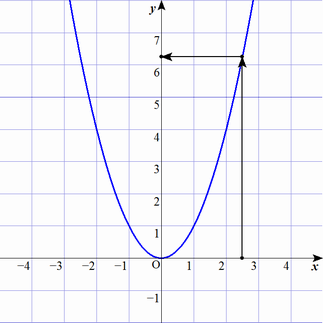
「出力 $y$ は 入力 $x$ の平方(2乗)」このルールは関数として扱えます。
数式で書くと $f(x)=x^2$ です。図で書くと次のようになります。
$x$ を決めると $y$ は1つに定まります。
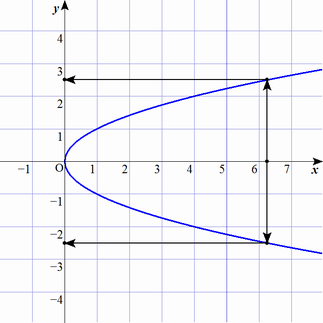
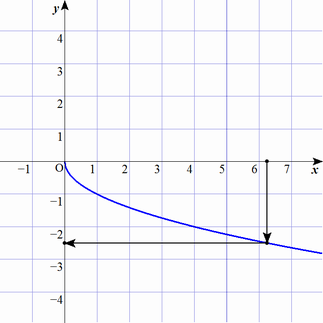
「出力 $y$ は 入力 $x$ の平方根」このルールは関数として扱えません。
数式で書くと $f(x)=\pm\sqrt{x}$ です。図で書くと次のようになります。
$x$ を決めても $y$ は1つに定まらなくて、何を出力するのか決まりません。
「出力 $y$ は 入力 $x$ の平方根2つのうち正の方(ルート)」このルールは関数として扱えます。
数式で書くと $f(x)=\sqrt{x}$ です。図で書くと次のようになります。
$x$ を決めると $y$ は1つに定まります。
「出力 $y$ は 入力 $x$ の平方根2つのうち負の方」このルールは関数として扱えます。
数式で書くと $f(x)=-\sqrt{x}$ です。図で書くと次のようになります。
$x$ を決めると $y$ は1つに定まります。
「出力は1つだけ」に限定しないと、関数を組み込んだ数式に答えが複数出てしまって、数式の答えがどんな数値になるのか定まらない、ということになってしまうからです。
例えば $\sin(x)\cos(x)$ という数式で $\sin(x)$ の出力が2種類あったとすると、この数式がどんな数値を表すのか定まりません。
もっと発展した話では多価関数という出力が2つ以上あるような話も出てきますが、基本的には出力を1つに限定したもののみを関数として扱います。
二変数関数
出力は1つに限るのですが、入力変数は2つ(2種類)あって構いません。
このような関数を二変数関数といいます。
入力数値を $(x, y)$ の組で表します。
出力数値を $z$ で表します。
$(x, y)$ と $z$ がどのような関係になってるかというルールを $f$ で表します。
\begin{align*}
\mbox{入力数値の組}\quad \left(\begin{array}{c}x \\ y\end{array}\right) \quad\xrightarrow[\mbox{関係ルール}]{f}\quad z \quad\;\mbox{出力数値}
\end{align*}
「$f$ というルールで $(x, y)$ と $z$ の関係がつきます」ということを数式で表現したものが以下の式になります。
\begin{align*}
z = f(x, y)
\end{align*}
二変数関数の例として次の関数を考えてみましょう。
\begin{align*}
f(x, y) = x^2 + y^2
\end{align*}
この関数に $(1, 2)$ を入力すると $5$ が出力されます。
この関数に $(3, 3)$ を入力すると $18$ が出力されます。
出力は1つに定まってます。
多変数関数
出力は1つに限るのですが、入力変数はいくつあって構いません。
2つ以上の入力変数をもつ関数を多変数関数といいます。
入力数値を $\left(x_1, x_2, \cdots , x_n\right)$ の $n$ 個の数値の組で表します。
出力数値を $y$ で表します。
$\left(x_1, x_2, \cdots , x_n\right)$ と $y$ がどのような関係になってるかというルールを $f$ で表します。
\begin{align*}
\mbox{入力数値の組}\quad \left(\begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n\end{array}\right) \quad\xrightarrow[\mbox{関係ルール}]{f}\quad y \quad\;\mbox{出力数値}
\end{align*}
「$f$ というルールで $\left(x_1, x_2, \cdots , x_n\right)$ と $y$ の関係がつきます」ということを数式で表現したものが以下の式になります。
\begin{align*}
y = f\left(x_1, x_2, \cdots , x_n\right)
\end{align*}
プログラムや表計算アプリで使われる関数
表計算アプリ Excel での関数の基本は(関数について)を見てください。
コンピュータ内部では2進法で表現される数値の2進数を使って情報を扱っています。
情報処理は入出力を基本に行います。
様々な情報処理の方法を関数としてまとめることで、複雑な情報処理を関数の組み合わせによって簡単にすることができるようになります。
指数関数 対数関数 対数目盛
桁違いに大きな数や小さな数を扱うときは、指数関数や対数関数が便利です。
(指数 対数)で指数関数や対数関数、対数目盛について説明しています。
演算と聞いて思い浮かべるのは足し算、引き算、掛け算、割り算の四則演算です。
演算は関数として扱うことができますので、以下のように適当な関数名をつけてみましょう。
\begin{align*}
2+3&=5 \qquad\fbox{$+$ 演算子の左の項の数値 $2$ と右の項の数値 $3$ を入力して、数値 $5$ を出力} \\
\mathrm{puls}(2,3)&=5 \qquad\fbox{←のように表記する}
\end{align*}
\begin{align*}
2-3&=-1 \qquad\fbox{$-$ 演算子の左の項の数値 $2$ と右の項の数値 $3$ を入力して、数値 $-1$ を出力} \\
\mathrm{mins}(2,3)&=-1 \qquad\fbox{←のように表記する}
\end{align*}
\begin{align*}
2\times 3&=6 \qquad\fbox{$\times$ 演算子の左の項の数値 $2$ と右の項の数値 $3$ を入力して、数値 $6$ を出力} \\
\mathrm{tims}(2,3)&=6 \qquad\fbox{←のように表記する}
\end{align*}
\begin{align*}
2\div 3&=0.5 \qquad\fbox{$\div$ 演算子の左の項の数値 $2$ と右の項の数値 $3$ を入力して、数値 $0.5$ を出力} \\
\mathrm{divs}(2,3)&=0.5 \qquad\fbox{←のように表記する}
\end{align*}
これらの演算は2つの項を結びつけるという意味で2項演算といいます。
「2つの数値を入力して、それを元に何らかの操作で、1つの数値を出力する」と捉えると二変数関数の役割をこなしていることが分かります。
演算とは数や数の組を元に、数を作り出す操作です。
単項演算というのもあります。
こちらの方も、以下のように適当な関数名をつけてみましょう。
\begin{align*}
-(4)&=-4 \qquad\fbox{$-$ 演算子(符号反転演算子)の右の項の数値 $4$ を入力して、数値 $-4$ を出力} \\
\mathrm{reve}(4)&=-4 \qquad\fbox{←のように表記する}
\end{align*}
\begin{align*}
-(-4)&=4 \qquad\fbox{$-$ 演算子(符号反転演算子)の右の項の数値 $-4$ を入力して、数値 $4$ を出力} \\
\mathrm{reve}(-4)&=4 \qquad\fbox{←のように表記する}
\end{align*}
\begin{align*}
+(4)&=4 \qquad\fbox{$+$ 演算子(符号そのまま演算子)の右の項の数値 $4$ を入力して、数値 $4$ を出力} \\
\mathrm{stay}(4)&=4 \qquad\fbox{←のように表記する}
\end{align*}
\begin{align*}
+(-4)&=-4 \qquad\fbox{$+$ 演算子(符号そのまま演算子)の右の項の数値 $-4$ を入力して、数値 $-4$ を出力} \\
\mathrm{stay}(-4)&=-4 \qquad\fbox{←のように表記する}
\end{align*}
\begin{align*}
\sqrt{4}&=2 \qquad\fbox{$\sqrt{}$ 演算子(平方根演算子)の中の数値 $4$ を入力して、数値 $2$ を出力} \\
\mathrm{sqrt}(4)&=2 \qquad\fbox{←のように表記する}
\end{align*}
「1つの数値を入力して、それを元に何らかの操作で、1つの数値を出力する」と捉えると一変数関数の役割をこなしていることが分かります。
二項演算を二変数関数、単項演算を一変数関数として考えて、今までに習った公式を関数と関数の関係として見直してみましょう。
\begin{align*}
\mathrm{plus}(a,b) = \mathrm{plus}(b,a) \qquad\fbox{足し算の交換則}
\end{align*}
\begin{align*}
\mathrm{mins}(a,b) \neq \mathrm{mins}(b,a) \qquad\fbox{引き算の交換則は成り立たない}
\end{align*}
\begin{align*}
\mathrm{plus}(\mathrm{plus}(a,b),c) = \mathrm{plus}(a,\mathrm{plus}(b,c)) \qquad\fbox{足し算の結合則}
\end{align*}
\begin{align*}
\mathrm{mins}(\mathrm{mins}(a,b),c) \neq \mathrm{mins}(a,\mathrm{mins}(b,c)) \qquad\fbox{引き算の結合則は成り立たない}
\end{align*}
\begin{align*}
\mathrm{tims}(a,b) = \mathrm{tims}(b,a) \qquad\fbox{掛け算の交換則}
\end{align*}
\begin{align*}
\mathrm{divs}(a,b) \neq \mathrm{divs}(b,a) \qquad\fbox{割り算の交換則は成り立たない}
\end{align*}
\begin{align*}
\mathrm{tims}(\mathrm{tims}(a,b),c) = \mathrm{tims}(a,\mathrm{tims}(b,c)) \qquad\fbox{掛け算の結合則}
\end{align*}
\begin{align*}
\mathrm{divs}(\mathrm{divs}(a,b),c) \neq \mathrm{divs}(a,\mathrm{divs}(b,c)) \qquad\fbox{割り算の結合則は成り立たない}
\end{align*}
\begin{align*}
\mathrm{tims}(\mathrm{plus}(a,b),c) = \mathrm{plus}(\mathrm{tims}(a,c),\mathrm{tims}(b,c)) \qquad\fbox{分配則}
\end{align*}
\begin{align*}
\mathrm{plus}(a,\mathrm{reve}(b)) = \mathrm{mins}(a,b)
\end{align*}
\begin{align*}
\mathrm{mins}(a,b) = \mathrm{reve}(\mathrm{mins}(b,a))
\end{align*}
\begin{align*}
\mathrm{tims}(a,\mathrm{reve}(b)) = \mathrm{reve}(\mathrm{tims}(a,b))
\end{align*}
記号の使い方を変えただけなのですが、自分の頭で考えてみると、これまでに曖昧にしていた様々なことが、はっきりしてくると思います。
また、関数の表記法にも慣れますので、頭の体操だと思って色々やってみることをお勧めします。