
「条件によって違った操作を実行したい」というときに使うのが「IF関数」です。「IF(イフ)」は英語では「もしも~ならば」という意味を表す接続詞です、「~」の部分が条件をあらわしています。Excelでは条件が真(正しい)か偽(正しくない)かによって実行処理を変えたい場合に「IF関数」を使います。
例題用のファイル 基礎例題4 を右クリックしてUSBメモリに保存してください。
余裕がある人は、話を聞きながら手を動かして例題を解いてください。
余裕がない人は、話を聞くのに集中してください。 後で余裕のある時に、ここの解説を読みながら例題に取り組んで、分からないところを質問してください。
IF関数は以下のような形式で扱います。
3つの引数があることに注意してください。引数の順番も重要です。それぞれの引数には次の内容を入力します。
論理式は「もし~が真ならば」の「~」の部分の条件を表す式です。 いくつか例をあげます。
| 例 | 意味 |
|---|---|
| A1>=10 | A1の出力が10以上 |
| A4<35 | A4の出力が35未満 |
| B2=C3 | B2の出力とC3の出力が同じ |
| D4="○" | D4の出力が○ (数式内では、文字列データはダブルクォーテーション記号「"」で括る) |
| E3="" | E3の出力が何もない (「""」は空文字を表してる) |
| SUM(E3:E7)=10 | セル範囲「E3:E7」の合計が10 |
条件式に使われる等号や不等号などの記号は比較演算子と呼ばれるもので、比較演算子を挟んだ左辺と右辺を比較します。以下にExcelで使える比較演算子をまとめておきます。
| 比較演算子 | 読み方 | 意味 |
|---|---|---|
| = | 等しい (equal) | 左辺と右辺が等しい |
| > | より大きい (greater than) | 左辺の方が右辺より大きい |
| >= | より大きいか等しい (greater or equal) | 左辺の方が右辺より大きい、又は左辺と右辺が等しい |
| < | より小さい (less than) | 左辺の方が右辺より小さい |
| <= | より小さいか等しい (less or equal) | 左辺の方が右辺より小さい、又は左辺と右辺が等しい |
| <> | 等しくない (not equal) | 左辺と右辺が等しくない |
第2引数には条件式が真の時、第3引数には条件式が偽の時にIF関数が処理する内容を記述します。
内容は「数値データ」、「文字列データ」、「数式」、「関数」など通常のセルに入力する出来る内容なら何でも構いませんが注意が1つだけあります。 「数値データ」に関してはそのまま数値を「123」のように打ち込めば良いのですが「文字列データ」に関してはダブルクォーテーション記号「"」で括って「"文字列"」のように書く必要があります。
「数式内に記述する文字列はダブルクォーテーションで括る」と覚えてください。
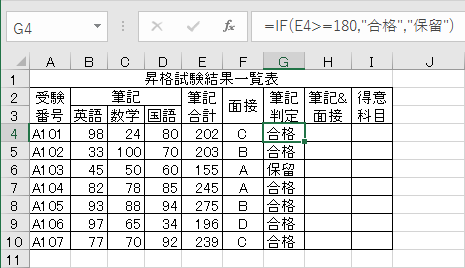
表の確認:筆記試験の合計点を元に合格判定をします。

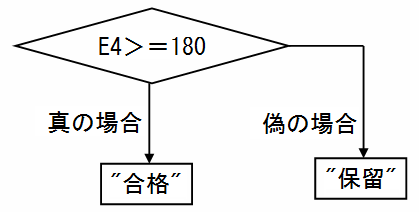
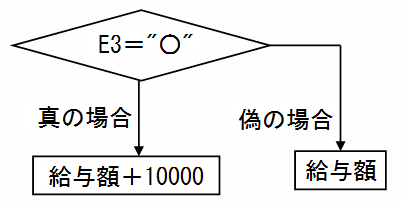
フローチャート
処理の流れを下図のように説明したものがフローチャートです。 上から順に線を辿っていって処理を実行します。 今後IF関数を複雑に組み合わせた分岐が出てきた時、便利に使えますので今のうちに慣れておきましょう。
菱形の部分に分岐の為の条件式がかかれています。 条件式を判定した結果が真なら下の矢印に、偽なら右の矢印に処理が分岐します。
操作手順
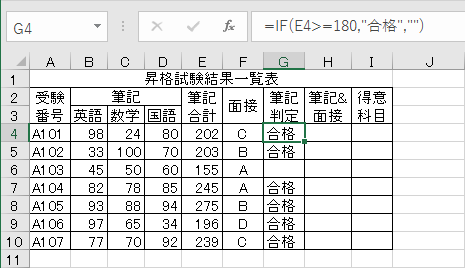
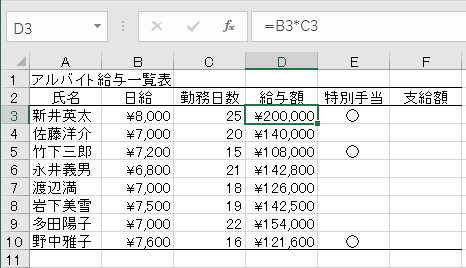
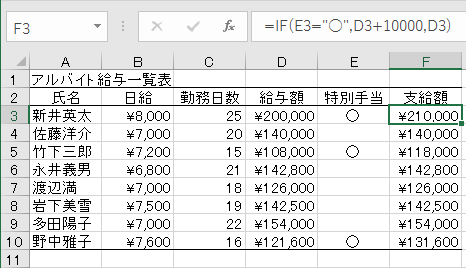
特別手当がもらえるならば¥10,000増額し,そうでなければ「日給*勤務日数」のみの給料を支払います。
フローチャート
操作
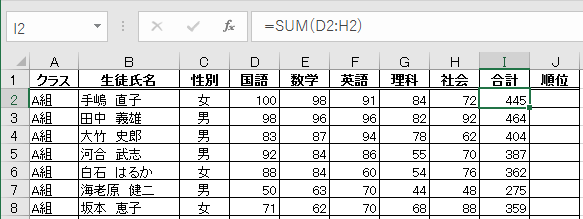
ランキング(ranking)という言葉を聞いたことがあると思いますが、ランク(rank)とは順位のことです。あるセルの値が全体の何番目かを知りたい時にRANK.EQ関数が使えます。
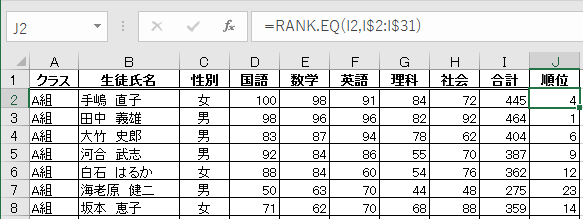
RANK.EQ(ランク、ドット、イコール)関数は以下のような形式で扱います。
順位には「降順」と「昇順」があります。
降順(大きい順) 9→1 のように降りて行く順
昇順(小さい順) 1→9 のようにに昇って行く順
全生徒の5科目の成績合計を元に、順位を計算します。
Excel 2007 以前の古いバージョンには、順位を求める関数に RANK 関数しかありませんでした。
RANK 関数は、Excel 2010 以降では RANK.EQ 関数に名前が変わりました。 (互換性を確保するため古い RANK 関数は2010以降でも使えます。)
また、Excel 2010 以降から新たに RANK.AVG(ランク、ドット、アベレージ) 関数が追加されました。
RANK.EQ と RANK.AVG は同順位の扱いが違います。
3位のデータと4位のデータが同じ値なら RANK.EQ 関数ではどちらも3位になりますが、RANK.AVG 関数ではどちらも平均順位の3.5位になります。
3位のデータと4位のデータと5位のデータが同じ値なら RANK.EQ 関数では3つとも3位になりますが、RANK.AVG 関数では3つとも平均順位の4位になります。