増加率（変化率）について

目次

はじめに
目次へ↑

ある量が基準になる量に対してどれくらいの割合で増加したのか（変化したのか）を増加率（変化率）で表します。 変化率も増加率も同じものです。

増加率などの割合を計算するには、掛け算や割り算の感覚をきちんと身につけておかなければなりません。 小学校、中学校で習ってると思いますがここでしっかり復習しておきましょう。 大学生になった今復習することでより理解が深まります。

増加率（変化率）とは
目次へ↑

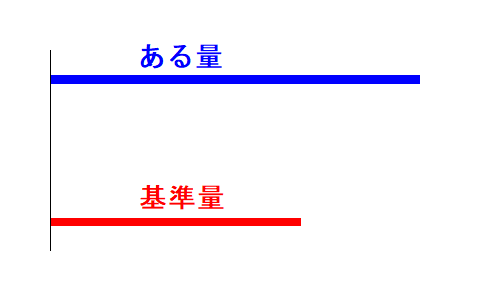
ある量を下の絵の青い棒の長さで表します。 基準量を赤い棒の長さで表します。

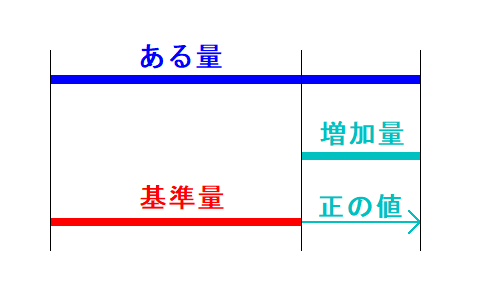
ある量が基準量に対してどれくらい増えているのかは増加量で表されます。

\begin{align*} \color{#00c0c0}{\text{増加量}} = \color{blue}{\text{ある量}} - \color{red}{\text{基準量}} \qquad\cdots (*) \end{align*}

増加率は増加量が基準量の何倍か（何割か）で表されます。 つまり、増加量を基準量で割ることによって、増加率が得られるのです。

\begin{align*} \text{増加率} = \frac{\color{#00c0c0}{\text{増加量}}}{\color{red}{\text{基準量}}} \end{align*}

この式の増加量の部分に $(*)$ 式を代入して整理すると次のような式になります。

\begin{align*} \require{cancel} \text{増加率} &= \frac{\color{blue}{\text{ある量}} - \color{red}{\text{基準量}}}{\color{red}{\text{基準量}}} = \frac{\color{blue}{\text{ある量}}}{\color{red}{\text{基準量}}} - \frac{\cancel{\color{red}{\text{基準量}}}}{\cancel{\color{red}{\text{基準量}}}} \\ &= \frac{\color{blue}{\text{ある量}}}{\color{red}{\text{基準量}}} - 1 \end{align*}

負の増加率（負の変化率，減少率）とは
目次へ↑

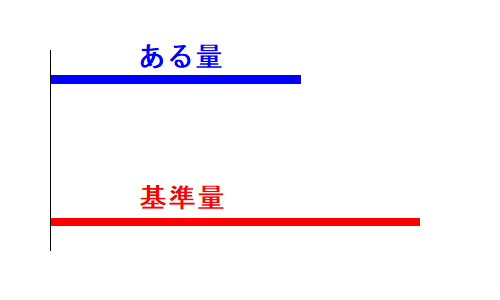
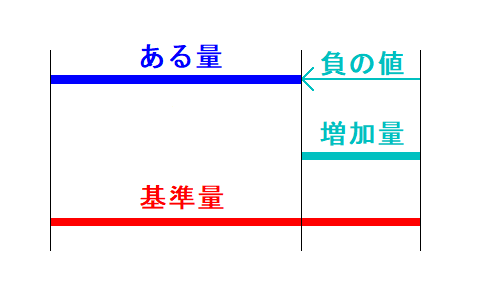
基準量の方が大きい時を考えてみましょう。

$(*)$ 式を計算してみましょう。増加量の計算結果は負（マイナス）になります。 負の増加量のマイナス符号を取ったものを減少量と言うことがあります。（例えば、増加量が$-3$なら$3$が減少量）
\begin{align*} \color{#00c0c0}{\text{増加量}} = \color{blue}{\text{ある量}} - \color{red}{\text{基準量}} \qquad\cdots (*) \end{align*}
増加率の計算式は同じですが、計算結果の符号に注意しましょう。
\begin{align*} \text{増加率} = \frac{\color{#00c0c0}{\text{増加量}}}{\color{red}{\text{基準量}}} = \frac{\color{blue}{\text{ある量}}}{\color{red}{\text{基準量}}} - 1 \end{align*}
基準量の方が大きい時、倍率と呼ばれる $\frac{\color{blue}{\text{ある量}}}{\color{red}{\text{基準量}}}$ の部分が $1$ より小さくなるので、増加率の計算結果の値は負になります。 （$1$より小さい倍率を歩合と言うことや割合と言うことがあります。） 負の増加率のマイナス符号を取ったものを減少率と言うことがあります。

倍率とは
目次へ↑

ある量が基準量の何倍になるのか、ということを倍率と言います。 倍率とはある量を基準量で割った量です。

\begin{align*} \color{green}{\text{倍率}} = \frac{\color{blue}{\text{ある量}}}{\color{red}{\text{基準量}}} \end{align*}

増加率と倍率の間には次の関係があります（自分で手を動かして導出してみましょう）。

\begin{align*} \text{増加率} &= \color{green}{\text{倍率}} - 1 \\ \color{green}{\text{倍率}} &= 1 + \text{増加率} \\ \end{align*}
上の二つ式の $1$ の部分は $\frac{\color{red}{\text{基準量}}}{\color{red}{\text{基準量}}}=1$ から導かれた部分なので、歩合で $10$割と書いて表したり、百分率で $100\%$ と書いて表した方が分かりやすいかも知れません。 $100 \%$ の基準に増加率を加えた値が倍率になります。

「基準量」を $1$割増加させた「ある量」を作ってみましょう。 この場合は増加率が $0.1$ で、倍率が $1.1$ です。 \begin{align*} \text{ある量} &= \text{基準量}\times\text{倍率} \\ &= \text{基準量}\times\left(1 + \text{増加率}\right) \\ &= \text{基準量}\times\left(1 + 0.1\right) \\ &= \text{基準量}\times 1.1 \\ \end{align*}

「基準量」を $1$割減少させた「ある量」を作ってみましょう。 この場合は増加率が $-0.1$ で、倍率が $0.9$ です。 \begin{align*} \text{ある量} &= \text{基準量}\times\text{倍率} \\ &= \text{基準量}\times\left(1 + \text{増加率}\right) \\ &= \text{基準量}\times\left(1 - 0.1\right) \\ &= \text{基準量}\times 0.9 \\ \end{align*}

「基準量」を $1$割増加させた「ある量」をさらに $1$割減少させた「とある量」を作ってみましょう。 \begin{align*} \text{とある量} &= \text{ある量}\times\left(1 - 0.1\right) \\ &= \text{基準量}\times\left(1 + 0.1\right)\times\left(1 - 0.1\right) \\ &= \text{基準量}\times\left(1 - 0.1^2\right) \\ &= \text{基準量}\times\left(1 - 0.01\right) \\ &= \text{基準量}\times 0.99 \\ \end{align*} 「基準量」を$0.1$ 増加させて、さらに$0.1$ 減少させた「とある量」は、「基準量」に対して $-0.01$ の増加率（$0.01$の減少率）、$0.99$の倍率の量になります。

ここのでの話が（複利計算）や（ネイピア数）の話に繋がっていく面白いところです。

増加率（変化率）の例
目次へ↑

授業ではある量をその年の CPI（消費者物価指数）、基準になる量を前年の CPI にとって、インフレ率を計算してます。 他にも GDP（国内総生産） の変化率や失業率の変化も計算してます。

以下の例は、みなさんの生活に密着した感覚の増加率です。

掛け算、割り算と割合
目次へ↑

割合や割り算がどのような意味を持っているのか忘れてしまった人は今のうちに思い出しておいて下さい。 今後の人生で必要不可欠になるものです。

割合とは２つの量を比べたときに一方が他方の何倍にあたるかという関係のことです。

ここでは割合（何倍）に注目して掛け算と割り算の関係を復習します。
掛け算や割り算には割合以外にも、長さの単位を持った量を２つ掛けて面積の単位を持った量を作り出すというような『新しい単位を作り出す』性質もありますが、ここでは扱いません。

$2$ が $3$つ で $6$ になる（$2$ の $3$倍 は $6$）ということを掛け算で書くと次のようになります。

\begin{align*} \color{red}{2}\times \color{green}{3} = \color{blue}{6} \end{align*}
同じことなんですが $6$ の中には $2$ が $3$つ 入っている（$6$ は $2$ $3$倍 だ）ということを割り算で書くと次のようになります。
\begin{align*} \color{blue}{6}\div \color{red}{2} = \color{green}{3} \end{align*}

このように掛け算と割り算は３つの量の関係を違った見方で表している式なのです。 『何倍なのかという倍率を知りたいときは割り算を使う』というように目的に応じて使い分けます。

次に上の例の、$2$を基準量、$6$をある量、$3$を倍率という言葉で書き換えてみます。

\begin{align*} \color{red}{\text{基準量}}\times \color{green}{\text{倍率}} = \color{blue}{\text{ある量}} \\ \color{blue}{\text{ある量}}\div \color{red}{\text{基準量}} = \color{green}{\text{倍率}} \end{align*}
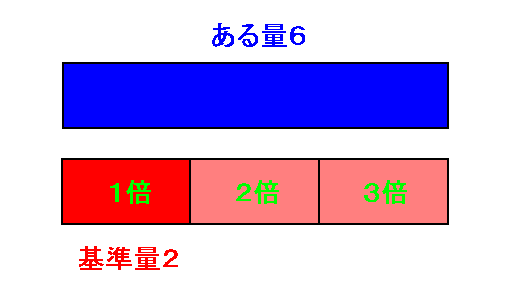
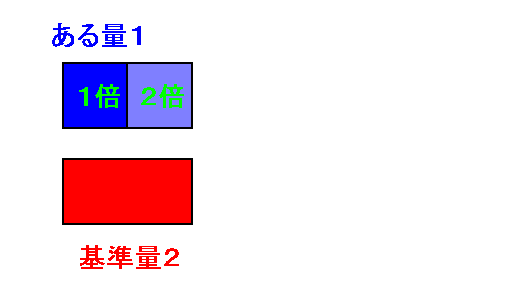
絵で書くと次のような感じです。ある量$6$ は 基準量$2$ の $3$倍 です。 言い換えますと、基準量$2$ の $3$倍 が ある量$6$ になります。

倍率には『基準量とある量に同じ量を掛けたり割ったりしても倍率は変わらない』という性質があります。 倍率を計算する式の割り算は次のように分数で書き表すことができます。

\begin{align*} \color{green}{\text{倍率}} = \frac{\color{blue}{\text{ある量}}}{\color{red}{\text{基準量}}} \end{align*}
分数で表現すると、先ほどの性質は『分数の分母と分子に同じ量を掛けたり割ったりしても値は変わらない』という性質になります。 例えば分母分子に $2$ を掛けると次のようになります。
\begin{align*} \color{green}{3} = \frac{\color{blue}{6}}{\color{red}{2}} = \frac{\color{blue}{6}\times 2}{\color{red}{2}\times 2} = \frac{\color{blue}{12}}{\color{red}{4}} \end{align*}
自分で上のような絵をある量が$12$、基準量が$4$、の場合で描いてみてください。 その場合でも基準量$4$ の $3$倍 がある量$12$ になることが確認できて納得できると思います。

今度は分母分子を $4$ で割ってみましょう。 次のようになります。

\begin{align*} \color{green}{3} = \frac{\color{blue}{6}}{\color{red}{2}} = \frac{\color{blue}{6}\div 4}{\color{red}{2}\div 4} = \frac{\color{blue}{\frac{3}{2}}}{\color{red}{\frac{1}{2}}} = \frac{\color{blue}{1.5}}{\color{red}{0.5}} \end{align*}
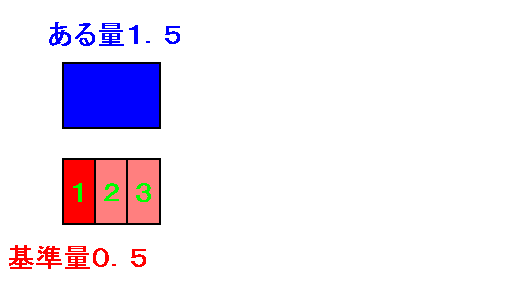
（$2$分の$1$）分の（$2$分の$3$）、もしくは$0.5$分の$1.5$になります。 この場合を絵で描くと次のようになります。
この場合も基準量$0.5$の$3$倍がある量$1.5$になってます。

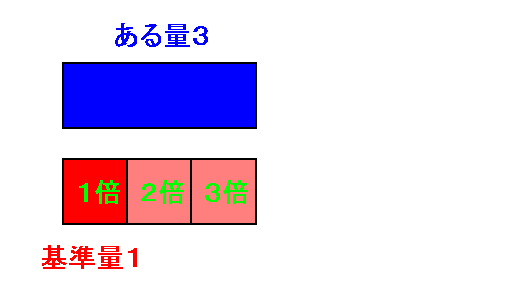
基準量（分母）を$1$にすることによって、ある量の部分（分子の部分）がそのまま倍率を表す数値になります。 これを『一当たり量』といいます。

\begin{align*} \color{green}{3} = \frac{\color{blue}{6}}{\color{red}{2}} = \frac{\color{blue}{6}\div 2}{\color{red}{2} \div 2} = \frac{\color{blue}{3}}{\color{red}{1}} \end{align*}

また、基準量（分母）を$100$にすると、ある量の部分（分子の部分に）百分率（百当たり量）が出てきます。 百分率はパーセント$(\%)$とも言います。
ちなみに千分率パーミル$(\unicode{x2030})$、一万分率パーミリアドなんてのもあります。

\begin{align*} \color{green}{3} = \frac{\color{blue}{6}}{\color{red}{2}} = \frac{\color{blue}{6}\div 2\times 100}{\color{red}{2} \div 2\times 100} = \frac{\color{blue}{300}}{\color{red}{100}} \end{align*}
このように$6$割る$2$は$3$倍になりますが、百分率では$300\%$となります。

『一当たり量』等を使って基準量を変えて考えると、ある量の方が基準量より小さいときや、 ある量が基準量で割り切れないとき、つまり倍率が整数じゃない場合でも理解できるようになります。 例えば、ある量が$2$、基準量が$4$の場合は次のように倍率が$0.5$倍（$2$分の$1$倍）になります。

\begin{align*} \frac{\color{blue}{2}}{\color{red}{4}} = \frac{\color{blue}{2}\div 4}{\color{red}{4}\div 4} = \frac{\color{blue}{\frac{1}{2}}}{\color{red}{1}} = \frac{\color{blue}{0.5}}{\color{red}{1}} \end{align*}
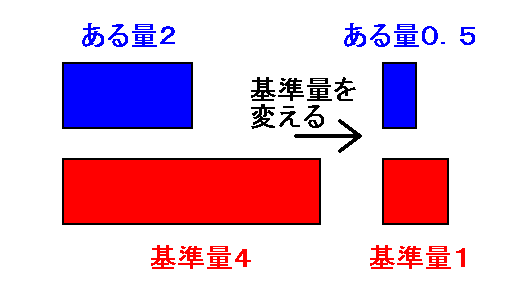
上の右の絵から基準量を$2$分の$1$倍（$0.5$倍）すればある量になるということが分かります。 これでも感覚が掴めない場合は、逆に見れば理解できるのではないでしょうか？。 今までは分母の部分を基準にしていましたが、今度は分子の部分を$1$にするように考えてみましょう。
\begin{align*} \frac{\color{blue}{2}}{\color{red}{4}} = \frac{\color{blue}{2}\div 2}{\color{red}{4}\div 4} = \frac{\color{blue}{1}}{\color{red}{2}} = \color{green}{0.5} = \color{green}{\frac{1}{2}} \end{align*}
つまり、ある量が基準量の$2$分の$1$倍であるということは、基準量の中にある量が$2$個入るということを表してます。 ここでもう一度この節の最初の式を見直してみましょう。
\begin{align*} \color{red}{\text{基準量}}\times\color{green}{\text{倍率}} &= \color{blue}{\text{ある量}} \\ \color{green}{\text{倍率}} &= \frac{\color{blue}{\text{ある量}}}{\color{red}{\text{基準量}}} \end{align*}
次に、上の一つ目の式で両辺を倍率で割ります。 上の二つ目の式では両辺の分母分子をひっくりかえします。 すると上の二つの式は次の二つの式になります。
\begin{align*} \color{blue}{\text{ある量}}\times\color{green}{\frac{1}{\text{倍率}}} &= \color{red}{\text{基準量}} \\ \color{green}{\frac{1}{\text{倍率}}} &= \frac{\color{red}{\text{基準量}}}{\color{blue}{\text{ある量}}} \end{align*}
この式である量と基準量の役割を入れ替えてある量の方を基準に見ると、倍率が逆数（倍率分の一）になるということが分かります。

小数の倍率を見て感覚が掴めない場合は「$10$分率」「$100$分率」「$1000$分率」など、基準量を切りの良い数字で考えてください。 例えば倍率$0.375$を考えると次のようになります。

\begin{align*} \color{green}{0.375} = \frac{\color{blue}{375}}{\color{red}{1000}} = \frac{\color{blue}{3}}{\color{red}{8}} \end{align*}
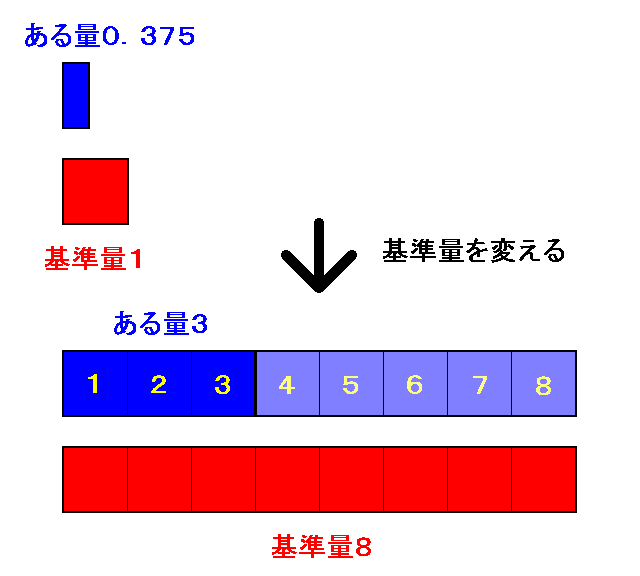
一つ目の等式では基準量を$1000$にとってます。$1000$当たりの$375$になります。 二つ目の等式では分母分子を$125$で割って基準量を$8$にとってます。 $8$当たりの$3$という量です。 分母分子にいろんな量を書けたり割ったりして、自分の分かりやすい数字に直して感覚を掴んでください。
また、倍率$3.375$など中途半端な倍率も $1000$分の$375 $と切りの良い数字で考えてみてください。 大体の大きさを知りたいときは倍率を $3+0.375$ のように整数部分と小数部分に分けて考えるのも、 どれくらいの倍率なのか感覚を掴むのには良い練習になります。

ここまで割合について説明してきましたが、一番のポイントは分母分子に同じ数を掛けたり割ったりして自分の扱いやすい形に直すということです。 これが分かっていれば分数の割り算なんかも簡単にできます。 例としてある量を $3$分の$2$という基準量 で割って倍率を求めてみましょう。

\begin{align*} \color{green}{\text{倍率}} = \frac{\color{blue}{\text{ある量}}}{\color{red}{\frac{2}{3}}} = \frac{\color{blue}{\text{ある量}}\times\frac{3}{2}}{\color{red}{\frac{2}{3}}\times\frac{3}{2}} = \frac{\color{blue}{\text{ある量}\times\frac{3}{2}}}{\color{red}{1}} \end{align*}
二番目の等式で分母分子両方で$3$を掛けて$2$で割りました（$2$分の$3$を掛けた）。 これによって基準量が$1$になり、倍率はある量に$2$分の$3$を掛けたものになります。 つまり「$3$分の$2$で割る」ということは「$2$分の$3$を掛ける（逆数を掛ける）」ことと同じであることが理解できます。

(イン活TOPに戻る)   (藤本の担当講義に戻る)   (目次に戻る)