Pareto の法則について

目次

はじめに
目次へ↑

ここでは Pareto の法則について説明します。 その前に準備としてベキ関数や指数と対数について復習します。 指数や対数は高校生の時に数学IIで習っています。 指数や対数についての詳しい解説がありますので興味のある人は見ておいてください。 ちなみにここでの指数はベキ指数の意味の指数で、消費者物価指数や土地価格指数などの指数とは別の意味です。 消費者物価指数など基準を100にとった時の比率の方は英語で index と言います。 べき指数の方は英語で exponent と言います。 元々は違う意味なんですが日本語では同じ漢字を当てています。

ベキ関数
目次へ↑

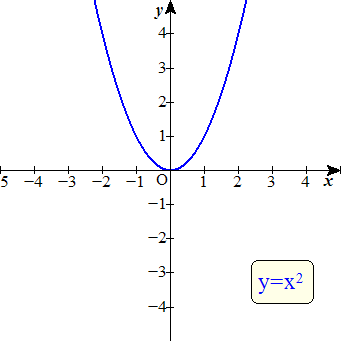
$x^2, x^3, \cdots$ のような「$x$の○○乗」のことを「累乗」や「ベキ乗」と呼びます。 （「ベキ」は漢字で「冪」と書きます。略字で「巾」という字を使うこともあります。） ベキ乗の肩に乗っている数値（$x^2$ なら「2」のこと）をベキ指数と呼びます。 マイナスのベキは逆数のことを表します。例えば $x$ のマイナス2乗は $x$ の2乗分の1と同じ意味になります （ $x^{-2} = \frac{1}{x^{2}}$ ）。 以下の図はベキ関数のグラフです。下のボタンでベキ指数をいろいろ変えてみて下さい。


ベキ指数は整数値だけではなく、実数値を取ることもできます。 例えば $x$ の $0.5$ 乗は $x$ の $\frac{1}{2}$ 乗と同じ意味になり、2乗して $x$ になる数なので $x$ の平方根（ルート）と同じ意味になります（ $x^{0.5} = x^{\frac{1}{2}} = \sqrt{x}$ ）。 以下の図はベキ関数のグラフです。下のボタンでベキ指数をいろいろ変えてみて下さい。 ベキ指数が整数ではないときは、$x$ が負の領域で $y$ が実数にならないので表示されません（$y$ は実数ではなく、実数と虚数を組み合わせた複素数になります）。

Pareto の法則
目次へ↑

高額所得者データを使って、Pareto（パレート）の法則が「日本の個人所得分布」について成立しているか？を検討しています。Paretoの法則とは、100年以上前（1897年）にイタリアの経済学者Paretoによって見出された法則です。彼は、当時のイギリスの個人所得が

\begin{align*} P(x) = cx^{-a} \end{align*}
に従っていることを発見しました。ここで、$x$ は所得金額、$c$ は定数、$P(x)$ は所得金額Xの人の番付（上位から数えた累積人数）です。この関係が成立する理由は、今でも明確には理解されていません。 しかし、フラクタルという概念と関係することは確からしく、特に $x$ の肩にある $a$ は Pareto 指数 と呼ばれます。

ここでいうフラクタルとは、何でしょうか？ なかなか難しい概念なのですが、ヒトコトで言うと自己相似になっている系をフラクタルと呼びます。 よく使われる例は、木や葉っぱのように同じパターンが繰り返される系です。 同じパターンが繰り返されるということは、あるパターンを見てもその大きさ（スケール）が分からない事を意味します。 言葉を換えると、フラクタルとはスケールを持たない系の事です。上の式は、まさにコレを反映するように作られています。

これを確かめてみましょう。 ここで例として、$x \rightarrow 10 x$ としてみます。このとき上の式の右辺は

\begin{align*} c(10x)^{-a} = c(10)^{-a}x^{-a} = c'x^{-a} \end{align*}
と変形できます（ここで、$c(10)^{-a}$ を改めて $c'$ と書き直しました）。 これより、$x$ のスケールを（10倍に）変えた場合も、パレートの法則を意味する数式は形を変えないことが分かります。 すなわち、この数式で表される系には特徴的なスケールが存在しないのです。 ちょっと難しくなりますが、スケール変換しても形を変えない分布はこの関数形しか存在しないことも証明できます。

つまり、個人所得分布に関してパレートの法則が成り立つと言うことは・・・
パレートの法則で記述される人たちには、所得に関するスケールが存在しないと理解できます。 彼らにとっては、所得に関しては1万円と10万円の区別が無いのです！ このような人たちは、高額所得者と呼ばれます。 パレートの発見後、様々な国の異なる年に対して法則が成立することが確認されています（講義では最近の日本について確認しました）。 そしてパレート指数 $a$ は、およそ1.5～2.5程度の値になると報告されています。

このようなパレートの法則は，高額所得者に対してしか成立しません。 そうでない人（中・低額所得者）は、パレートの法則から逸脱するはずです。 つまり、中・低額所得者には所得に関するスケールが存在すると考えられます。 最初にこれを指摘したのはGibrat（ジブラ，1931年）でした。

対数目盛り
目次へ↑

以下の式はパレートの法則を $y = P(x)$ として書き直したものです。

\begin{align*} y = c x^{-a} \end{align*}
この式の両辺で対数を取ると次のようになります。
\begin{align*} \log_{10}y &= \log_{10}(cx^{-a}) &&\scriptsize\fbox{対数の公式 $\log_{10}AB = \log_{10}A + \log_{10}B$ を使う。} \\ &= \log_{10}c + \log_{10}x^{-a} &&\scriptsize\fbox{対数の公式 $\log_{10}A^B = B\log_{10}A$ を使う。} \\ &= \log_{10}c - a\log_{10} x \end{align*}
さらに上の式を $Y = \log_{10}y$ と $X = \log_{10}x$ と $C = \log_{10}c$ を使って書き直すと
\begin{align*} Y = -a X + C \end{align*}
という形の直線の式になります。

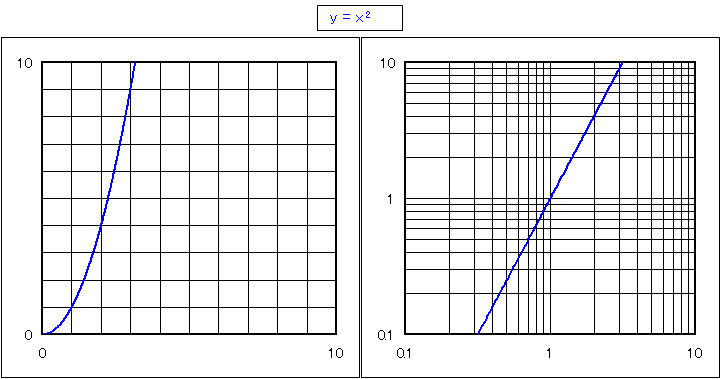
エクセルでは [軸の書式設定]→[目盛り]→[対数目盛りを表示する(L)] にチェックを入れると「対数軸目盛り」に変更されます。 エクセルで横軸と縦軸両方を「対数軸目盛り」にすると、横軸も $\log_{10}x$、縦軸も $\log_{10}y$ の縮尺で表示します。 次の図は様々なベキ関数を普通の目盛り（左図）と両対数の目盛り（右図）で表示したものです。 ボタンでベキ指数を切り替えてみてください。 右図の直線の傾きがベキ指数に対応します。


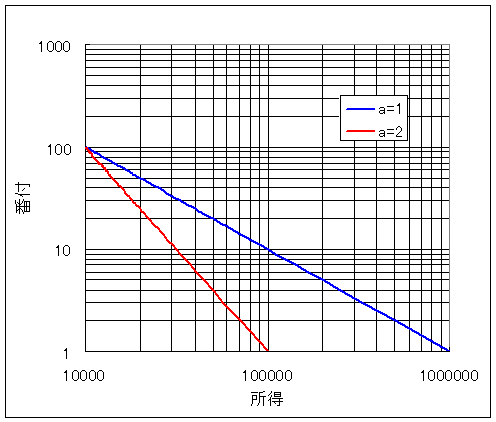
対数軸を使うと、パレートの法則は傾き $-a$ の直線として表現できます。 データが両対数軸で直線に乗っている場合はパレートの法則が成立しており、傾きの大きさを測ることによって、パレート指数を読み取ることができます。 そして、データが直線に乗らない場合は、パレートの法則は成立していません。 実際、中・低額所得者のデータは直線からずれています。

パレート指数の意味
目次へ↑

最後にパレート指数 $a$の意味をもう少し考えてみましょう。 パレート指数が大きいと、対数軸で考えた直線の傾きが大きく（急に）、パレート指数が小さいと、直線の傾きが小さく（ゆるやかに）なります。 この右下がり（$a>0$）の直線が「ゆるやか」だと、高額所得者の中でも超高額所得者が存在する割合が高くなることになります。 逆に直線が「急」だと、超高額所得者があまり存在しないと考えられます。

パレートの法則が成り立っている場合、格差の大きさとパレート指数の間に次のような関係が成り立ちます。

以下の図は簡単のために 100位 の人の所得が 10000 になるように固定した時の、1位から100位までパレートの法則が成り立っている場合の例を表しています。 赤線がパレート指数 $a=2$ の場合で、青線がパレート指数 $a=1$ の場合です。

$a=1$ の時は 1位と100位で所得が100倍違います。 $a=2$ の時は 1位と100位で所得が10倍違います。 つまりパレート指数は、高額所得者の中に超高額所得者が含まれる割合を示す指標となっています。

(イン活TOPに戻る)   (藤本の担当講義に戻る)   (目次に戻る)